Daylene Zielinski
Bellarmine University
Louisville, Kentucky
Abstract
As a mathematician teaching writing to freshmen, I have drawn on my experience with mathematics to create connections between the largely objective realm of the sciences and the more subjective realm of writing. I have constructed a multifaceted analogy bridging the gap between mathematics and writing designed to encourage my students to look at the process and end product of writing in a completely new and different manner. While my students are in the initial stages of their first formal writing assignment, I introduce them to what I call the geometry of a paper. I have had visual learners who were self-diagnosed poor writers say that for the first time they feel like they can “see” writing. Though this analogy may not be particularly illuminating for the student who already feels confident with the writing process, it has been of assistance to several of my students who need a different way to think about the process of writing a paper and how to conceptualize the result they are trying to produce. Many of these students decide that they understand writing better than they thought they did and that they can be good writers. This geometric structure also provides an alterative to the traditional outline that some students find helpful.
All college writing professors, even those of us coming from the sciences, are familiar with the basic mechanics of good writing such as parallelism, word precision, and the essential parts of an informative and readable paper: introduction, body, and conclusion. We have all heard, and perhaps heard ourselves repeat to our own students, the adage, “Tell ‘em what you’re gonna to tell ‘em. Tell ‘em. Then, tell ‘em what you told ‘em.” Shortly after I began teaching freshmen writing, I noticed that this basic tri-partite structure of good, cohesive writing repeats itself on several levels. As a mathematician teaching freshmen in a seminar course as part of the Interdisciplinary Core Curriculum at my institution, I began drawing on my experiences within my own discipline to help me teach writing. I soon found myself thinking about this tri-partite structure of writing in geometric terms since one of the most basic mathematical skills is pattern recognition. I have come to believe that this intrinsic, underlying structure is evocative of fractal geometry and that any well-written paper will exhibit the hallmarks of a particular fractal called the Koch curve. So, I began using this geometric object as a model for both the process of writing a paper and the final product of that process. I believe that this model could be of use to fellow scientists charged with writing instruction and more traditional humanities faculty who may be looking for new methods to connect to science majors taking their writing courses.
Geometry can be thought of as the study of the configuration of objects. A geometer studies the properties of those configurations that are intrinsic. An example that we all remember from high school is that there are 180˚ degrees in a triangle no matter how oddly it may be drawn (see Figure 1). Although triangles will play a role in the geometry encountered in this paper, we will need to discuss geometric objects that are a bit more complex than a simple triangle; these objects are fractals.
|
Figure 1: The sum of the measures of the angles of each of these triangles is 180˚ |
For the purposes of this paper, we will think of a fractal as a complex geometric object which exhibits the property of self-similarity. That is the somewhat curious property that if one magnifies an appropriate part of the object, one sees a similar structure to that of the whole and that this process can be repeated on several, sometimes infinitely many, levels of magnification. I have found that the best way to get my students thinking about self-similarity is to get them thinking about examples of this property that exist in nature. I ask them to think of the frond of a large fern and then imagine looking at one leaf on the frond. The leaf has the same structure as the entire frond. Even each blade of the leaf has tiny veins which mimic the structure of the larger frond. Similarly, a tree, branch, and twig all show the same general shape and structure, yet they exist on three different levels of magnification. I have never encountered a student for whom these images don’t evoke a reasonable understanding of self-similarity. These two examples illustrate why fractal geometry is often called the geometry of nature, since nature abounds with complex and often irregular shapes that nonetheless have an observable structure that is repeated on several levels of magnification (Mandelbrot, 1977).
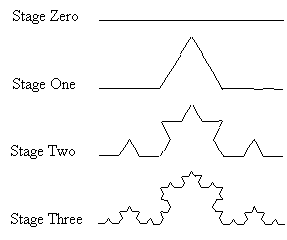
The particular fractal that I use in my writing analogy is the Koch curve. This curve is built through a sequence of approximations, none of which is the actual curve itself (see Figure 2). Any picture of the Koch curve is necessarily an approximation rather than the actual object since the curve is the culmination of an infinite process. However, just a few steps into the process will provide us with the general idea. We begin with a line segment one unit long. Next, we remove the middle third of the line segment and replace it with two sides of an equilateral triangle; this is the first stage of the Koch curve. The second stage is reached by removing the middle third of each of the line segments in the first stage and replacing them with two sides of an equilateral triangle. The Koch curve is the culmination of performing this process of removing the middle third of each line segment and replacing it with two sides of an equilateral triangle infinitely many times. The fifth stage approximation of the Koch curve shown in Figure 3 gives an adequate understanding of the complexity of this object. In fact the naked eye is hard pressed to discern the difference between stage five and any higher stage of development. Since I have been using this analogy, I have found that over half of my students in each class have heard of fractals before and many have at least a vague idea of what they are.
|
|
It should not surprise us that writing is, in many significant ways, intrinsically fractal. Writing is, after all, a complex and often irregular process that, in the final product, has an observable structure that repeats on several levels of magnification. A paper must have its introduction, body and conclusion. Paragraphs within the paper must have a topic, support for
|
|
that topic and a transition to the next paragraph. Sentences within each paragraph have a subject, verb and object. Thus, a well-written paper must exhibit the self-similarity displayed in Figure 4.
I tell my students to remember that the action is always in the middle referring to the bulk of a paper or paragraph and the verb of a sentence simultaneously. Yet, with this established we have only begun to mine the analogy between good writing and the Koch curve.
Figure 4: The self-similar structure of a paper.
Like creating a fractal, the process of writing is a sequence of approximations. At each stage both deletions and additions are introduced reorganizing the content and producing a more full and complete communication of ideas. Just as any depiction of the Koch curve is not the true object but some particular stage of the construction, the final version of any paper is not perfect communication but some advanced stage along the path to perfect communication, which is as unrealizable as any true geometric form. It is easy for a student to draw the analogy between successive drafts of her paper and successive stages of development of a fractal. Since many students find that fractal geometry piques their interest, they discover a new way to think about the writing process and a visual demonstration of the necessity of several drafts. After all, it is impossible to construct a detailed stage of the Koch curve without first passing successively through all previous stages of development. Since a developed stage of the Koch curve is analogous to the final version of a student’s paper, it can also be used as an alternative to a traditional outline.
Many students, even those who consider themselves good writers, dislike or are uncomfortable with the process of making an outline. However, when I provide them with a page that has the Koch curve running lengthwise down the left-hand side, most students are quick to see a correlation between the prominent points of the curve and the main points of their paper. I have included two labeled examples of these Koch curve based “outline” templates in the Appendix. The first is appropriate for a short paper or even a five-paragraph theme. The other can be used with a more complex paper and can be adapted for any assignment requiring from four to nine required elements in the body of the paper. A student can then easily construct a basic outline of her paper and check for the presence, or absence, of a rational flow and detectable organization to her ideas. This exercise also reinforces the structural self-similarity that should be present in the final paper. My students have commented that these templates make them feel more confident making an outline than when they begin with a blank page.
Each time I introduce these ideas, I always begin by asking a simple question with a counter-intuitive answer that I know will catch my students’ attention. I ask, “Can an object of infinite length fit inside a finite area?” Of course, their common sense screams that this is an absurdity, but they’ve been in school long enough to suspect that the answer must be yes since I bothered to ask the question. The answer is, indeed, yes, and the Koch curve has this peculiar property. Notice that at each stage of its development the curve is one-third longer than the stage before it (see Figure 2). This is because each time we remove the middle third of a line segment, we replace it with two segments the same length as that which we removed. This fact produces the sequence of lengths displayed in Figure 5, and produces another intriguing connection between the Koch curve and writing. With its limitless power to move, persuade, and inform with only finitely many words and symbols, writing also couches the infinite within the finite.
| Stage | 0 | 1 | 2 | 3 | … | n | … |
| Length | 1 | 4/3 | 16/9 | 64/27 | … | (4/3)n | … |
Figure 5: Lengths of several stages of the Koch curve.
I have found that about half, some semesters as many as two-thirds, of my seminar students enter the class feeling less than confident in their writing abilities for various reasons. The students who respond most favorably to this geometric presentation of writing are the visual learners who have never found a way to visualize the process of writing and those students who harbor the mistaken belief that writing is not a rational process. Pointing out the geometric structure of a paper allows these students to experience some of the essential parts of both the writing process and the final product of that process in a completely new manner that is more in synch with the way they prefer to learn. I make use of this geometric structure with at least one paper during each semester and encourage those who respond to it to continue to make use of it throughout my course. A few of my students have said that they will never think about writing
Reference
Mandelbrot, Benoit (1977). The Fractal Geometry of Nature. New York: W. H. Freeman and Co.
Author Note
The material in this paper gradually grew out of my experiences teaching writing in a Freshman Seminar course at Bellarmine University. I have taught various incarnations of my Mathematics and Culture Freshman Seminar at least once a year since the fall of 1999.
Correspondence concerning this article can be directed to Daylene Zielinski, Department of Mathematics, Bellarmine University, 2001 Newburg Road, Louisville, KY 40205. E-mail: dzielinski@bellarmine.edu.
This article first appeared in the Kentucky Journal for Excellence in College Teaching & Learning.